Try to Prove Math With Computers

Walking through an example!

I've written about formalising physics in PhysLEAN, and this month I’ve proved properties of a certain type of potential in quantum mechanics.

It’s pretty magical that we can prove things with computers, and I wanted to write up a toy example of my process in proving things in the LEAN language.

Given a goal that I want to prove, my approach is to repeatedly apply theorems through guessing, pattern matching, and trial and error.

In this post, I’ll be going through a really contrived example (which can be solved in one line now with standard libraries in Mathlib), but I think is instructive!

Suppose that I wanted to prove that 0 ≤ 2. First, I try to write this up as a goal. In LEAN, we have things called lemmas that represent minor statements that we wish to prove. The syntax looks like this.

lemma zero_leq_2 : 0 ≤ 2 := by

I’ve named what I want to prove, zero_leq_2, followed by the actual statement. Once we write this down, VS Code with LEAN will automatically initialise this as a ‘goal’. We want to solve this goal with tactics and pre-existing theorems. It’s like a game!

And from here, the game begins. We start searching for theorems that other people have written and try to apply it to our case. The main tool for that people use is Loogle, which is a way to search the big codebase of theorems.

Let’s say we’ve found these two theorems that look promising, that have already been proved by someone else.

lemma one_leq_two : 1 ≤ 2 :=

lemma zero_leq_n (a : ℕ) (h : 1 ≤ a) : 0 ≤ a := by

What do these mean?

one_leq_two says that 1 is less than 2, which is close to what we want, but not exactly.

zero_leq_n has more to it. The statements in brackets are hypotheses that need to be true to use the theorem. this case, we have two prerequisite hypotheses. First, a must be a natural number. Second, we need that 1 is less than a. This is then followed by the main assertion 0 ≤ a. If then hypothesis are true, then 0 is less than a.

This final statement looks like what we want, because the pattern 0 ≤ a matches our goal of 0 ≤ 2.

In LEAN, we use things called tactics. My most used tactic is apply, which resolves a goal if it the pattern of the statement an existing theorem. So in this case, we want to apply zero_leq_n to our current goal.

Let’s type this out and see what happens

lemma zero_leq_2 : 0 ≤ 2 := by

apply zero_leq_n

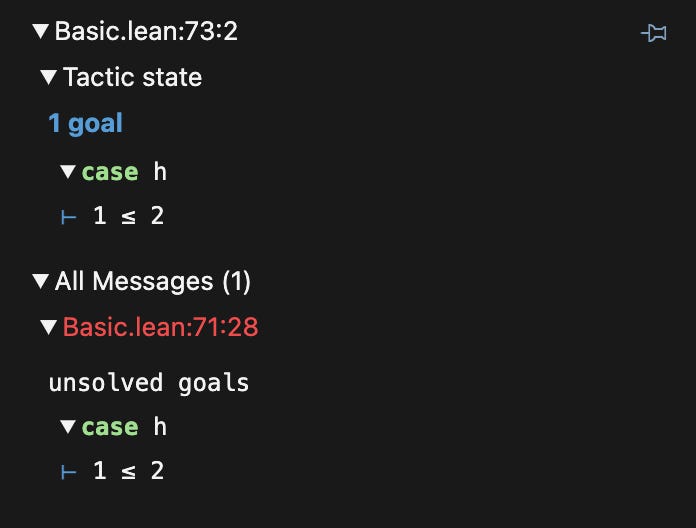
Once we do this, LEAN automatically recognises that the pattern of our goal matches the theorem - since 0 ≤ 2 matches 0 ≤ a. And so, it realises to set a = 2, so therefore progress is made. But are we done? Not quite!

Remember that in zero_leq_n,there is an additional hypothesis (h : 1 ≤ a) that has to be true. Since LEAN has set a = 2, it then asks us to prove the subgoal of 1 ≤ 2 that’s required. This creation of subgoals is super convenient in keeping track of things - all one has to do is just focus on solving goals till the end.

So, given our new goal of proving 1 ≤ 2, we can use the other theorem one_leq_two, to then resolve this goal.

lemma zero_leq_2 : 0 ≤ 2 := by

apply zero_leq_n

apply one_leq_two

Since the statement matches the goal exactly, we are done, and we’ve proved something new and cool!

An important point: in practice, people that work in LEAN use a standard library (Mathlib) to prove easy stuff like this with one liners, with stuff like the below!

import Mathlib.Tactic

example : 37 ≤ 1000000 := by
  norm_num